Zero-knowledge Proof Part 2

STACK-X Webinar — Introduction to Zero-knowledge Proof (Part 2)

The following article was adapted from a STACK-X Webinar conducted by Raymond Yeh, a software engineer at GovTech, on June 25, 2020.

This is the second post of a two-part series on Zero-knowledge Proofs. You can read the first part here.

 

Building your Zero-knowledge Proof (ZKP) circuit

In this post, we’ll be showing you how to build your own ZKP circuit from scratch. But before that, we have to decide which language we want to use.

If you ask around right now, you’ll find that your two main options are ZoKrates and Circom. We’ll be focusing on using ZoKrates today, but for your knowledge, here’s a quick breakdown of each language and their features:

ZoKrates:

High level ZKP library – you don’t need to know too much about the inner workings of a circuit to use it

Gentler learning curve – this is the easier language to pick up of the two if you’re a newcomer

Better tutorial – more user-friendly and understandable, with working examples within the tutorial

Tailored for blockchain use – ZoKrates was made to be used with blockchains and doesn’t have a web sdk yet

Circom:

Low level ZKP library – you’ll get to dive into the inner workings of circuits and write code similar to Verilog (if you’re familiar with this)

Steeper learning curve – this is definitely the harder language to pick up, since it’s more declarative than functional

Absence of tutorial – you have to learn via the various implementations and tests within the code

Not tied to blockchains – unlike ZoKrates, you’ll be able to use this for a wider variety of purposes

JavaScript – you can run tests in JavaScript, and Circom has a JavaScript Library for the development of web applications

From this breakdown, you can probably see why we’re opting to go with ZoKrates for an introductory tutorial.

Now, let’s get to visualising our circuit…

The task at hand

Let’s first recall the aim of our circuit.

We were previously trying to show that ZKPs could help a shopper to prove that they’re above the legal age limit for purchasing alcohol without revealing their actual age. 

Let’s start simple. What exactly am I trying to prove with age restrictions? Let’s take the legal age to be 21 and let’s take X to be our age.

You might therefore say that we’re trying to prove something like this:

‘I know of a number, X, that is greater than 21, but I won’t tell you what X is.’

Here’s how that circuit would look like:

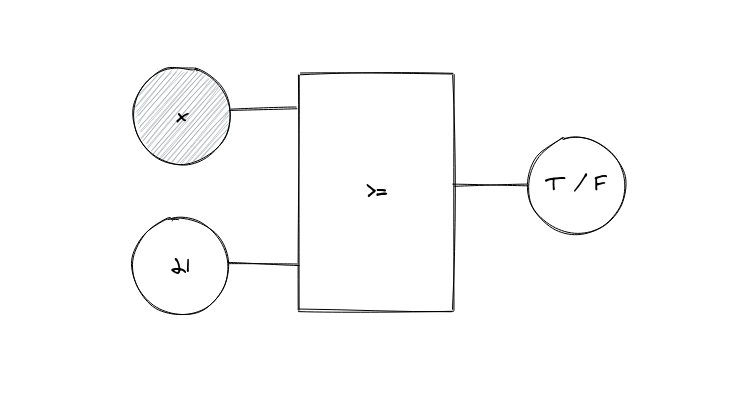
Our circuit simply calculates if X is ≥ 21. If it is, we get T and we’re granted permission to buy our beverage. This is, however, a little unsophisticated for our purposes. For instance, what if we want to apply this to a variety of products that might have different age restrictions?

Let’s take a second pass at this without specifying the precise age limit. This time let’s take X to be our birth year.

We could say we’re trying to prove that:

‘I know of a number, X, such that Y - X ≥ Z, where Y is the current year and Z is the age restriction. I won’t tell you what X is, but Y and Z are public knowledge.’

Again, here’s what that would look like:

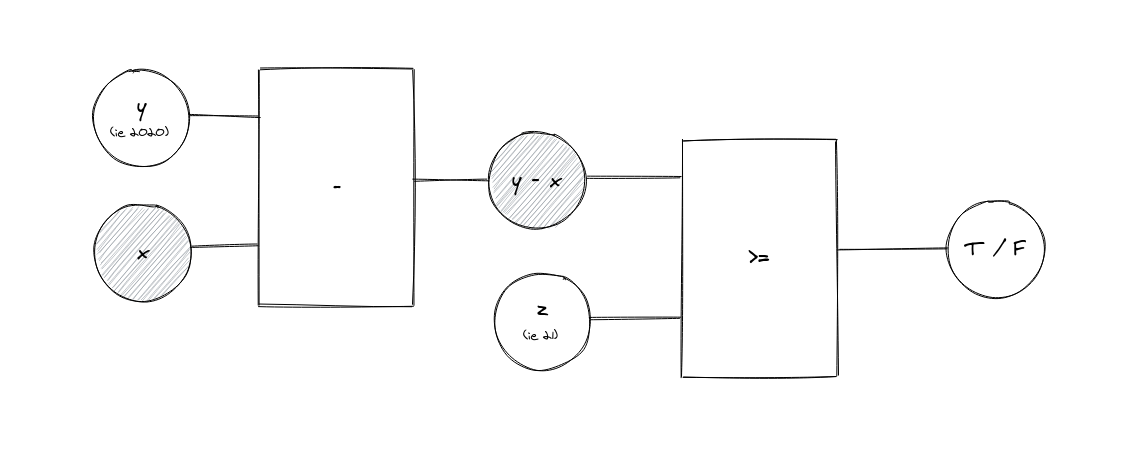
The circuit deducts our birth year from the current year to derive our age. From there, we compare our age with the legal age restriction, Z—if it’s ≥ Z, we get T.

This is a little better, but if you remember from Part 1, we wanted our circuit to include three public inputs. Y and X are public inputs, but we’re also missing something else: we’ll want to include information from an external source (say, a public national database, a smartcard, etc.) that can verify the claim that we are indeed born in the year X.

This brings us to attempt three. We’ll say that we’re trying to prove that:

‘I know of a number, X, such that F(X) = a, where a has been attested by the Government to be a valid piece of evidence about my age. I won’t tell you what X is, but you can verify a.’

Let’s have a look.

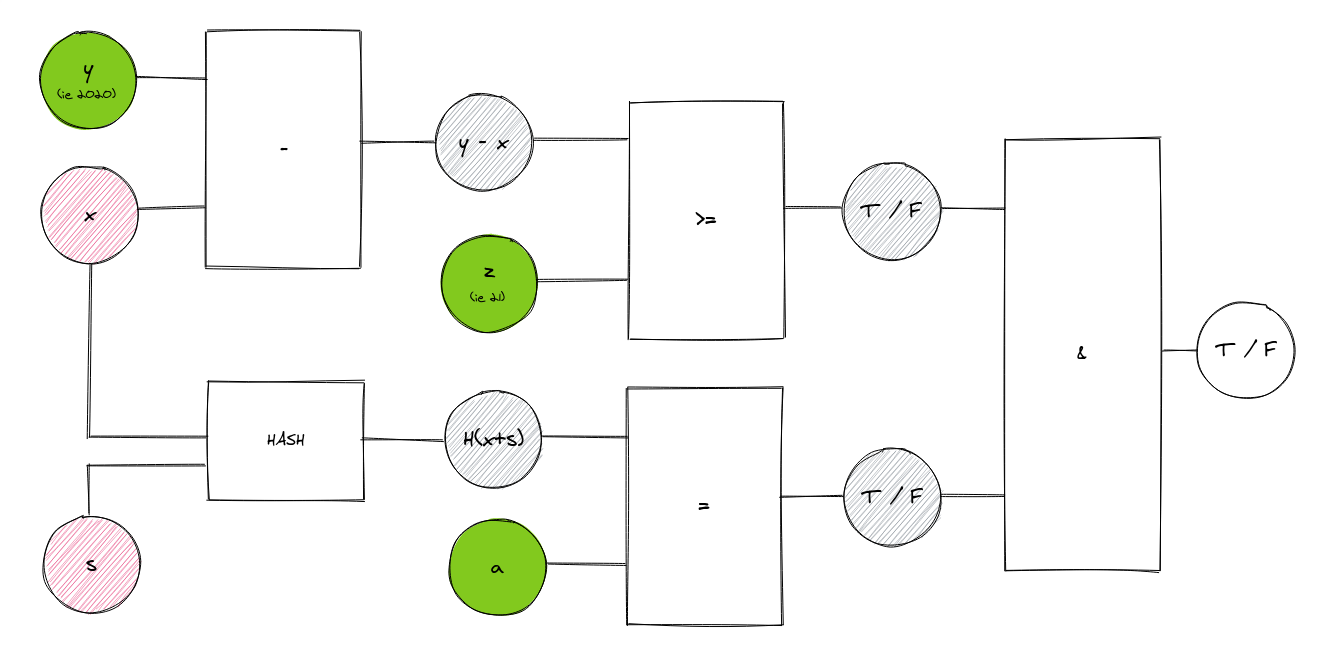
Remember hashing? When we talk about F(X) here, we’re really referring to the hashed output of X, or H(X +S) in the diagram. Our hashed X should match our hashed birth year, a, which uses the same inputs. This is how the cashier verifies that the birth year we provided is real.

Side note (for how this would work in practice): The hash we have, H(X + S), could perhaps be a string of values printed onto our identity card. We never have to show the cashier our birth year, only this hash. Being an officially-issued card, the hash here would match the hash used for our evidence of age, a, the government-attested piece of evidence.

Several things are happening in this circuit. Firstly, the same process as the previous circuit is taking place. Our age is derived from the subtraction of X from Y and it’s compared with Z. If it’s ≥ Z, we get our first T. However, X is also hashed along with a secret salt, S, so that we get H(X + S), which is then compared with a. If the value of X is determined to be equal to the evidence of our age, a, we get another T. If we get two Ts, it’s determined that we’re of legal age!

And that’s what our circuit should roughly look like.

Now we can finally get to coding.

Building our application — age check circuit

You can get started with ZoKrates by using the following Command Line Input for Linux, MacOS or FreeBSD:

curl -LSfs get.zokrat.es | sh

Now that you have everything set up, we can begin by working on the simplest component of our ZKP circuit: the age check circuit. To refresh your memory, this is what it looks like:

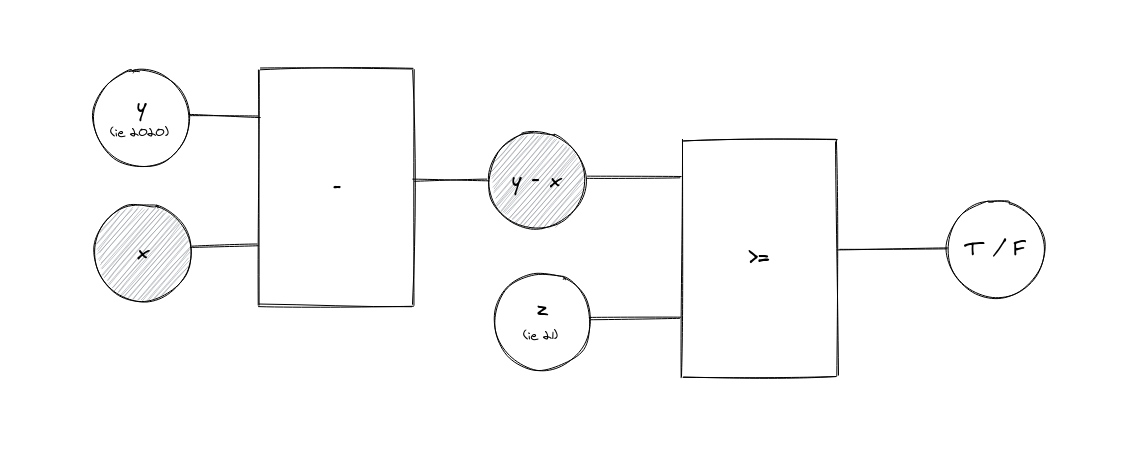
Using whichever code editor you’re familiar with, create a new directory and make a new file called ageCheck.zok. Copy and paste the following into your code editor:

def main(private field birthYear, field comparisonYear, field minimumDifference) -> (field):
      field result = if comparisonYear - birthYear >= minimumDifference then 1 else 0 fi
      return result

Let’s break this down a little. What we’re doing here is defining a function called main.

All this is doing is subtracting our birth year (which you’ll notice is a private field) from the comparison year (our current year). If the result is ≥ the minimum difference (21 in this case), then we get 1 (true). If not, we get a 0.

Now, we need to run this circuit. Assuming you already have ZoKrates up, run the following CLI in your terminal:

zokrates compile -i ageCheck.zok

After compiling, run the setup.

zokrates setup

You should now notice two new keys: the proving and verification keys. The former is used by the prover (i.e. us, the shopper), to generate the proof that they will share with the cashier. The cashier makes use of the latter key to verify this proof. Both keys are public—no sensitive data here.

zokrates compute-witness -a 1990 2020 21

What we’ve just done is compute our witness. A witness is, quite simply, one possible solution to our circuit. You’ll notice that each value stated here corresponds to the fields in our code: birth year (1990), comparison year (2020), minimum difference (21). If our inputs match these values, our circuit verifies this and produces a 1. 

zokrates generate-proof

We’ve just generated our proof for this circuit.

zokrates export-verifier

Finally, our verifier. Running this should have created a verifier.sol file. Your screen should now (hopefully) look something like this:

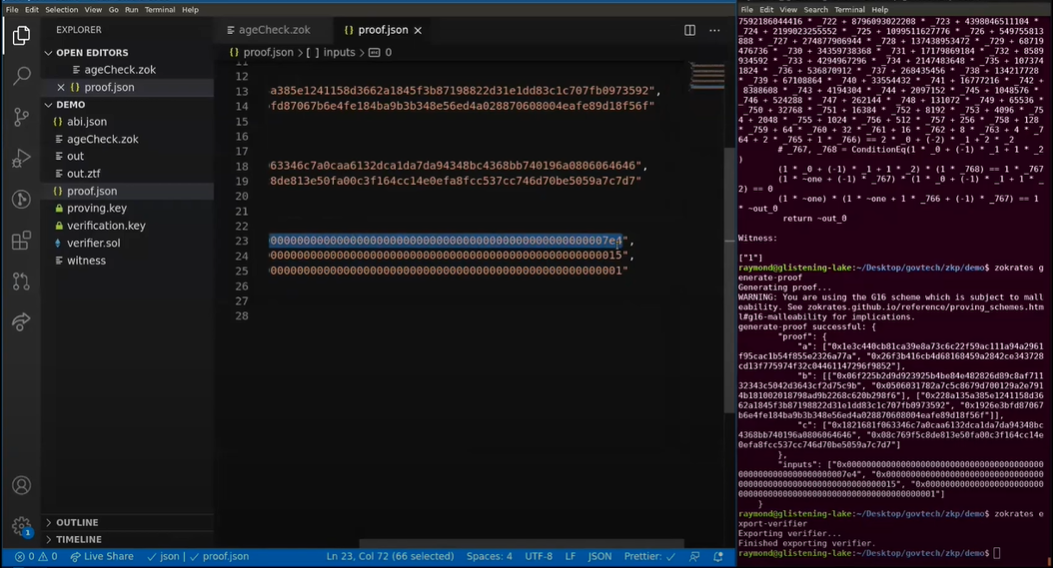
That’s it for this portion of the circuit, but it might be helpful to take a look at how this would work in action and ensure that everything is working fine.

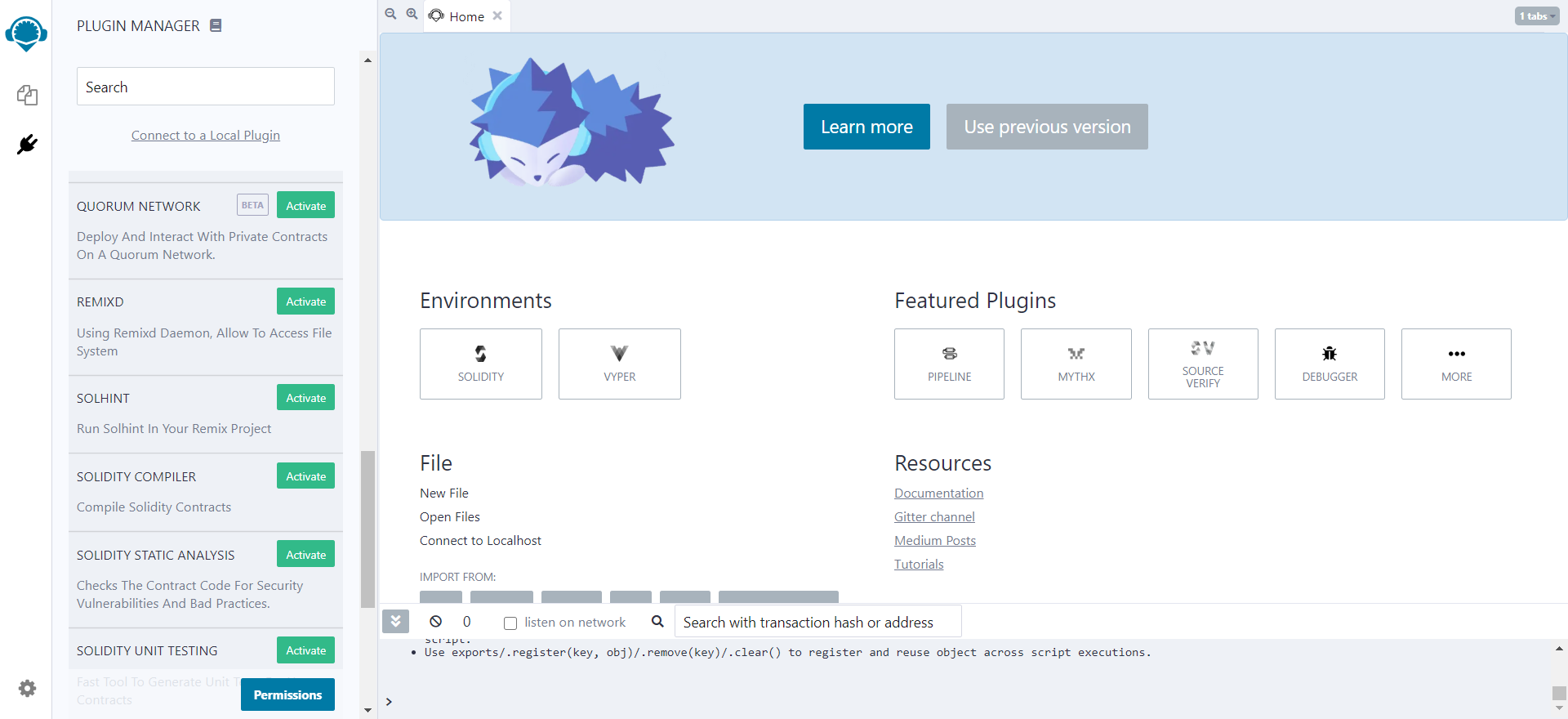
Copy the contents of our newly made verifier.sol file and head over to https://remix.ethereum.org/. You’ll want to click on Solidity under Environments, as that’s what we’ll be using:

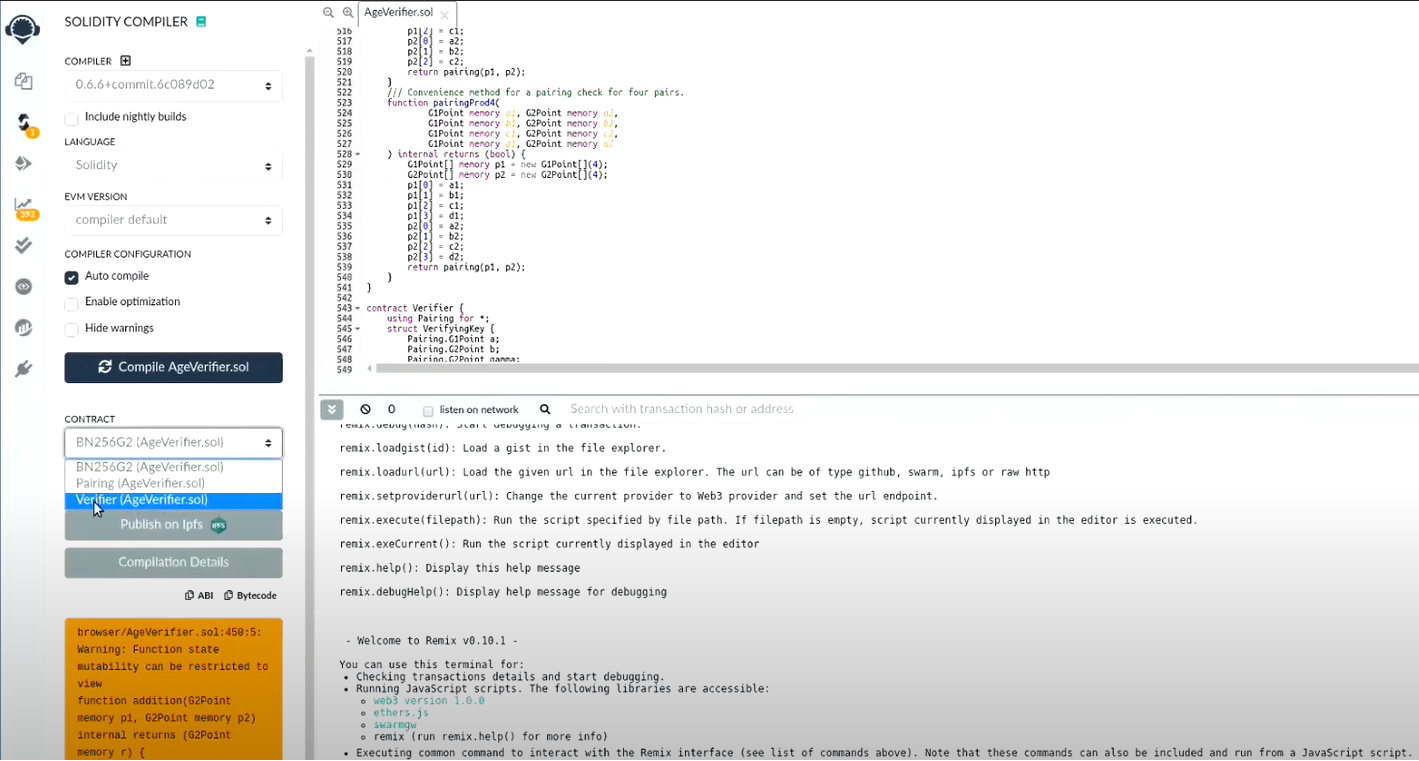
First, you’ll want to create a new file—let’s call it AgeVerifier.sol—and paste the lines of code into this. Now, you’ll want find the Solidity Compiler icon, click it and select the AgeVerifier.sol file. Compile this with the appropriate compiler version (you can find the pragma of the generated .sol on the first line of your file).

Next, head to your Deploy and Run Transactions plugin and deploy this verification contract onto your browser. If you’ve done this right, you should now see that our verifier has boxes labelled a, b, c and Input.

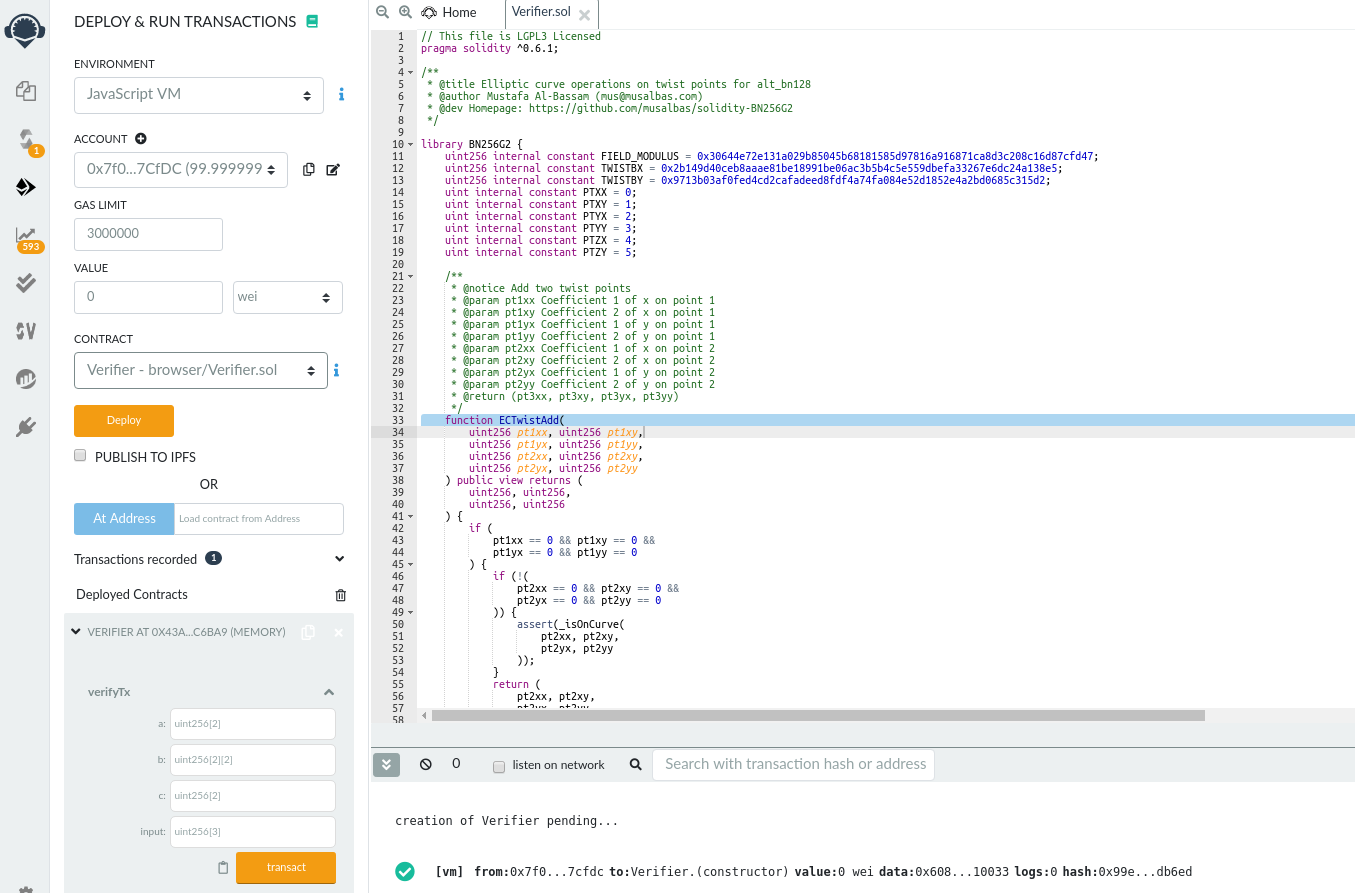
Heading back into your code editor and going into the proof we previously generated (proof.json), you’ll find each of these lines of code there. Copy and paste them into their respective boxes on Remix. Click on transact. You’ll see that our transaction has succeeded; based on the inputs, our circuit arrived at a T and our legal age status was verified.

So, what just happened here? If you take a closer look at the inputs box, you’ll notice these last few digits:

If you run them through a hexadecimal to decimal converter, you’ll realise that they actually correspond to 2020, 21 and 1 (this last one is just a bias signal that allows the circuit to run properly).

Also, remember a, b and c? Our private input, the birth year, was also run through this verifier via these lines of code. You’ll not be able to work backwards to derive the year from them, so don’t even bother trying! 

What we just did was run all these inputs, public and private, through our verifier, which then checked them and ensured that our minimum age was indeed 21.

With that, we’ve finished our first circuit!

Building our application — birth year check circuit

Moving on, we’ll now try to build the next portion of our circuit, which verifies that the prover knows of both the secret salt and birth year inputs only made available to him. This establishes that the prover is indeed the owner of the evidence of age published by the government. This needs to exist because without it, our shopper could simply lie about his birth year in order to get the alcohol.

Let’s create a new file and name this birthYearCheck.zok. Copy the following into your code editor:

import "hashes/sha256/512bitPacked" as sha256packed


  def main(private field birthYear, private field rand1, private field rand2, field hash1, field hash2) -> (field):
      h = sha256packed([0, birthYear, rand1, rand2])
      h[0] == hash1
      h[1] == hash2
      return 1

You may have noticed that we imported a package. This package is a hash function—specifically, the function SHA 256, which converts our birth year into a hash. You’ll actually see birth year listed as one of the private inputs, along with our secret salt (listed as rand1 and rand2). The government-published evidence of age, which is also hashed, is listed here as a public input (hash1 and hash2).

This runs a check to verify that the values are right. If the hashes correspond, it returns 1.

We now need to run several commands as per the previous circuit.

zokrates compile -i birthYearCheck.zok
zokrates setup
zokrates compute-witness -a 1990 123 123 233770742581153321658241226707865859106 161843013006795803511295431198461913882

If you look at the values in our witness, you can see that 1990 refers to the birth year, while 123 123 refer to our secret salt. The last string of digits refers to the hash that’s published online in our national database that verifies the birth year we provide. This witness, like before, serves as a sample solution for our circuit.

zokrates generate-proof
zokrates export-verifier

Now that this is done, we can repeat what we did for the age check circuit and see how this looks on Remix. You can just copy the verifier.sol that was generated and paste it over the existing ageverifier.sol on Remix. Repeat what we did before and compile this before deploying it to your browser.

Going into proof.json, we can copy a, b, c and inputs and paste them into the boxes on Remix. Hit transact and it should be verified.

As with the previous circuit, you’ll realise that our inputs actually correspond to our public inputs, namely the hashed evidence of age provided by our national database. Likewise, the contents of a, b and c correspond to our private inputs.

Remember that everything that we’re currently doing is on the protocol level. If we were building a real, user-friendly application, we would naturally need to abstract the process further so a user would not have to deal with any of this.

Building our application — the complete circuit

Finally, let’s finish our circuit by bringing our two component circuits together. Again, this is what it will end up looking like:

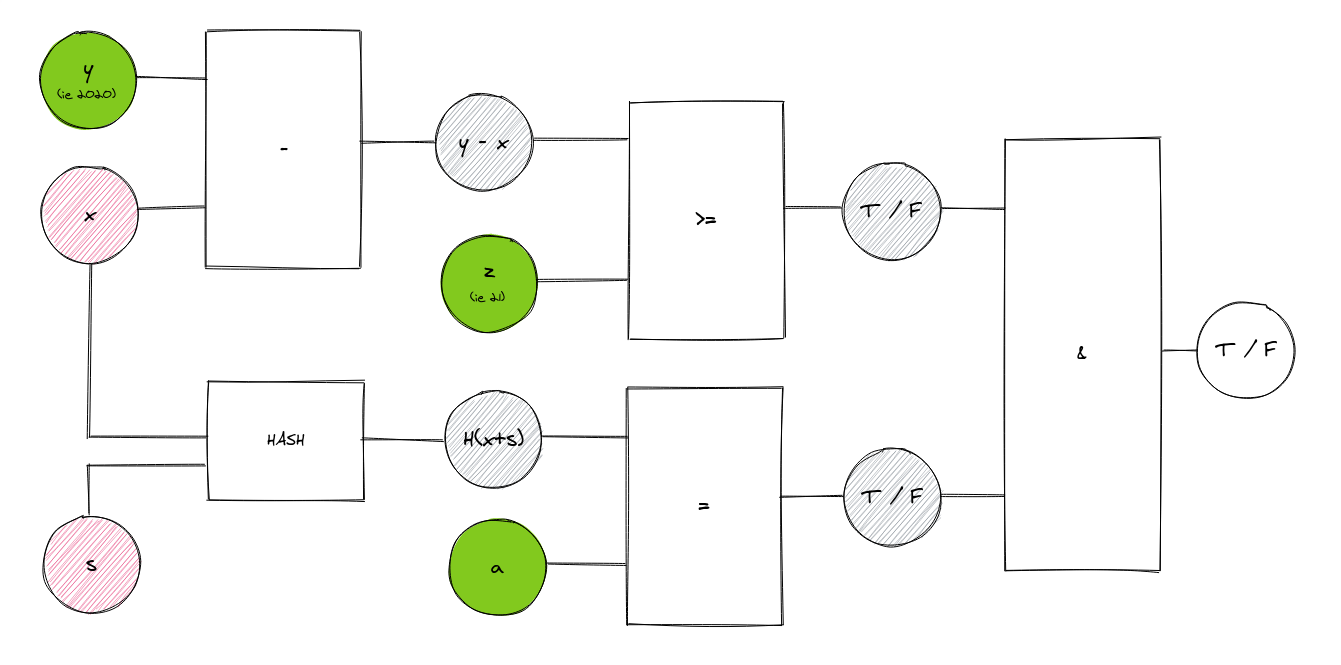
Let’s make a new file in our code editor and call this complete.zok. Copy the following into your editor:

import "hashes/sha256/512bitPacked" as sha256packed


  def birthYearCheck(private field birthYear, private field rand1, private field rand2, field hash1, field hash2) -> (field):
      h = sha256packed([0, birthYear, rand1, rand2])
      h[0] == hash1
      h[1] == hash2
      return 1

  def ageCheck(private field birthYear, field comparisonYear, field minimumDifference) -> (field):
      field result = if comparisonYear - birthYear >= minimumDifference then 1 else 0 fi
      return result

  def main(private field birthYear, private field rand1, private field rand2, field hash1, field hash2, field comparisonYear, field minimumDifference) -> (field):
      birthYearTest = birthYearCheck(birthYear, rand1, rand2, hash1, hash2)
      birthYearTest == 1
      ageTest = ageCheck(birthYear, comparisonYear, minimumDifference)
      ageTest == 1
      return 1

As you can see, we’ve incorporated our birthyear and age checks into the code. The first two portions are exactly the same as the previous two circuits we’ve worked on. Finally, at the bottom, if both of the previous functions are true, our circuit returns a 1, or true.

Now, let’s run our commands:

zokrates compile -i complete.zok
zokrates setup
zokrates compute-witness -a 1990 123 123 233770742581153321658241226707865859106 161843013006795803511295431198461913882 2020 21

Again, let’s look through our values. We have, in order, our birth year, our secret salt, our government-provided hash (or evidence of age), the current year, and finally our legal age (or minimum difference). These are all the inputs we need for this circuit. Finally:

zokrates generate-proof
zokrates export-verifier

We can finally take a look at how this will work back on Remix. Head back over, copy and paste the contents of your verifier.sol into your browser and compile it. Deploy this into your browser as usual, and then copy and paste a, b, c and your inputs from your proof.json file into the boxes under your Deployed Contracts.

If you’d like, you can take a closer look at our inputs on Remix:

Again, each line can be run through a hexadecimal to decimal converter if you want to find out what they correspond to. The first two lines are the hash provided by the government, while the subsequent lines refer to the same public inputs as before: 2020, 21 and 1, our bias signal.

In any case, if everything has been done correctly to this point, our circuit should have been verified…

…and that’s it! You can pat yourself on the back because you’ve successfully created a legal age ZKP circuit.

If you would like to have a look at the full library of code samples used in this exercise, you can head over to https://github.com/yehjxraymond/ZoKrates-experiment.

If you want to try following along with a video version of this workshop, or if you’d like to see this done with Circom instead of ZoKrates, you can find all the recorded webinars here.

Thanks for reading!

 

By Raymond Yeh and Michael Tan

Published on 22 July 2020.

Last updated 28 February 2023

---